Digital Filters
FIR Filter
This function block represents a FIR filter. These filters are one of two primary types of digital filters used in Digital Signal Processing (DSP) applications (the other type being IIR). "FIR" means "Finite Impulse Response".
You can realize the following functions with a FIR filter:
- Low-pass
- High-pass
- Band-pass
- Band-stop
Operation
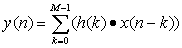
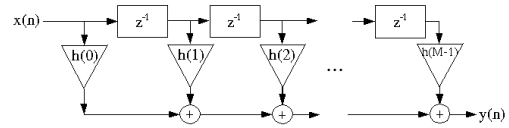
Parameters
Designs a finite impulse response (FIR) filter based on the windowing method. The windowing FIR filter design method is a straightforward technique implemented by expanding the frequency response of an ideal filter in a Fourier series and then truncating and smoothing the response using a window.
Window type: Hamming
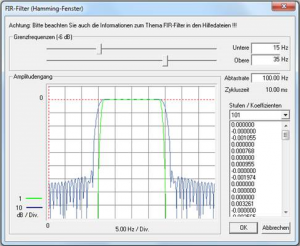
Sampling rate:
The sampling rate is the reciprocal of the cycle time.
Corner frequencies:
Low-pass:
Lower = 0 and
0 < Upper < half-the-sampling rate
High-pass:
0 < Lower < half-the-sampling rate and
Upper = half-the-sampling rate
Passband:
0 < Lower < Upper < half-the-sampling rate
Stopband:
0 < Lower < Upper < half-the-sampling rate
Tabs / Coefficients (filter order):
A FIR "tap" is simply a coefficient/delay pair. The number of FIR taps, is an indication of
1) the amount of memory required to implement the filter,
2) the number of calculations required, and
3) the amount of "filtering" the filter can do; in effect, more taps means more stop band attenuation, less ripple, narrower filters, etc.
Signals
| Name | I/O | Type(s) | Function |
|---|---|---|---|
| X | I | FLOAT | Input signal |
| Y | O | FLOAT | Output signal |
Comments
The calculation of a FIR-filter with a high number of coefficients (max. 999) requires substantial resources in the target system (device).
At the below marked reference values, means the sample (= synchronized measuring rate) and the number of coefficients, the shown number of filter blocks can be used in one application.
| Number of coefficients | Sampling rate 1000 | Sampling rate 500 | Sampling rate 200 | Sampling rate 100 |
|---|---|---|---|---|
| 101 | 4 | 20 | 40 | 100 |
| 251 | 2 | 8 | 16 | 40 |
| 501 | 1 | 4 | 8 | 20 |
| 999 | 0 | 2 | 4 | 10 |
These values are rough approximations. The real numbers depends on the performance of the target device, the complexity of the program and the use of other function blocks. Especially the application of other function blocks with demanding resource consumption (e.g. archive) can influence the number of usable filter function blocks significantly.